- Total
꿈꾸는리버리
[백준 알고리즘] 3053 직사각형에서 탈출 본문
문제: https://www.acmicpc.net/problem/3053
3053번: 택시 기하학
첫째 줄에는 유클리드 기하학에서 반지름이 R인 원의 넓이를, 둘째 줄에는 택시 기하학에서 반지름이 R인 원의 넓이를 출력한다. 정답과의 오차는 0.0001까지 허용한다.
www.acmicpc.net

풀이방법:
1. 유클리드 기하학
중고등학교때 기본적인 수학 공부를 한 사람이라면.. 알 거라 생각하기에 식만 적고 넘어가려한다.
원의 넓이 = R^2 * 3.141592 (R은 원의 반지름)
잘 모르는 사람이라면 다음 링크를 눌러 내용을 읽어보면 금방 이해가 갈 것이다.
https://m.blog.naver.com/kingforpoii/220741446639
5단원 원의 넓이(원의 넓이)
(2015년 수업) http://blog.naver.com/kingforpoii/220336772334 수학수업에는 2가지 접근 방법이 있다. 첫...
blog.naver.com
2. 택시 기하학
나는 백준 문제를 읽고 택시 기하학을 이해하지 못해서 구글링을 해봤다.
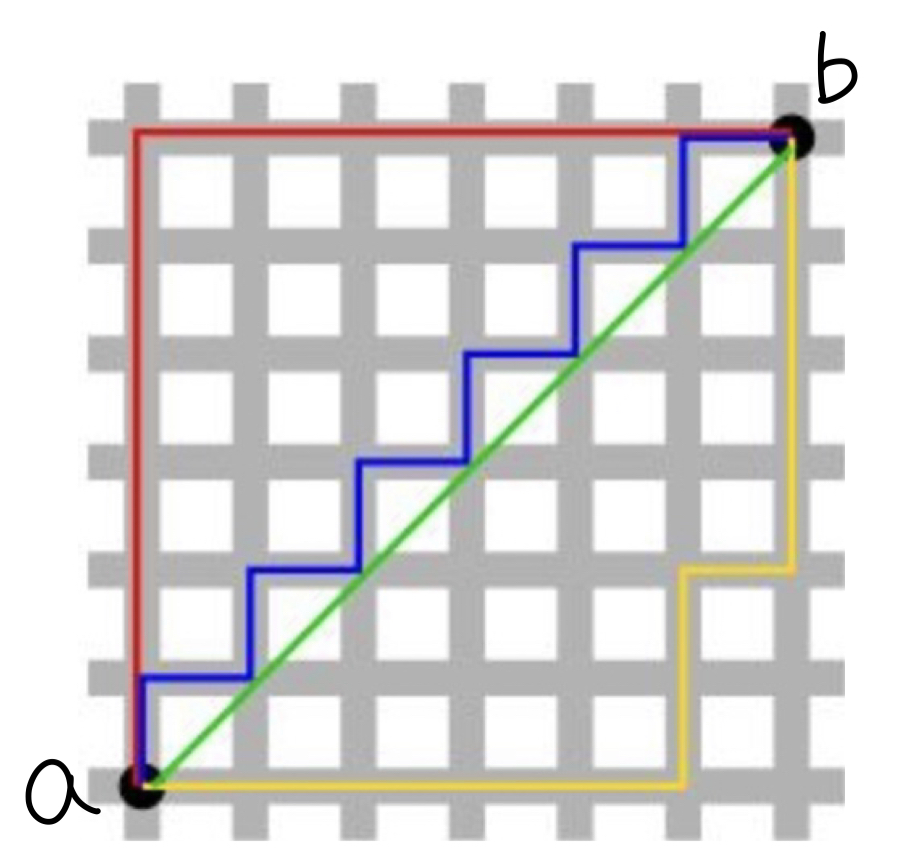
점 a에서 b로 갈 때 초록색으로 가면 최단이겠지만 흰 박스가 건물이라고 했을 때 택시드라이버 입장에서 생각해보면 ㅎㅎ.. 건물을 뚫고 갈 수는 없을 것이다. 그래서 흰 박스를 돌아서 a에서 b로 가야하는데 그 방법은 빨강, 파랑, 노랑으로 다양하다.
하지만 결국 도착했을 때 지나온 거리를 따져보면 x축으로 6칸, y축으로 6칸이라는 것을 알 수 있다.
" 택시 기하학에서 두 점 T1(x1,y1), T2(x2,y2) 사이의 거리는 다음과 같이 구할 수 있다.
D(T1,T2) = |x1-x2| + |y1-y2| "
백준에 있던 이 내용이 앞서 설명한 내용에 해당한다. 총 거리 = x축 6칸 + y축 6칸
자 그렇다면 택시 기하학을 원에 적용해보자 !
원이 무엇인가. "평면 위의 한 점에 이르는 거리가 일정한 평면 위의 점들의 집합으로 정의되는 도형"
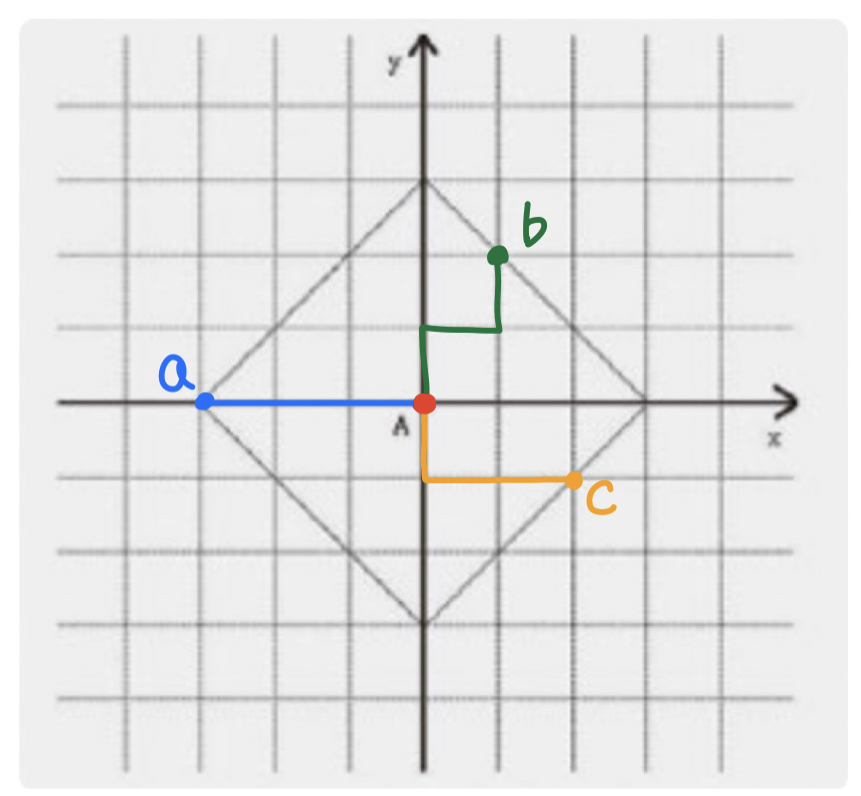
잘 생각해보면 아래의 마름모 모양이 만들어진다.
그 이유는 점 A에서 출발해 a,b,c 등의 점으로 이동을 할 때 거리 R 이라는 "일정한" 거리만큼 이동하기 때문이다. (R은 반지름의 길이)
우리가 구해야하는 것은 "택시 기하학에서 원의 넓이" !
->택시 기하학에서 원의 넓이는 대각선의 길이가 2R인 마름모가 된다.
따라서 택시 기하학에서 원의 넓이는 {(2*R)^2}/2 = 2*(R^2)
추가 ) 조정자의 사용
cout << fixed;
cout.precision(16); 의 의미
--->
cout.precision(n) 만 사용을 하면 3.14 같은 경우에는 n=3인 경우이다.
하지만
cout << fixed;
cout.precision(n) ; 을 하면 3.14 같은 경우에는 n=2인 경우이다.
즉, cout << fixed;를 해줘야지 소숫점 아래 자릿수의 개수를 설정해주는 것이 된다.
작성한 코드는 다음과 같다.
#include <iostream>
#include <math.h>
#include <iomanip>
#define pi 3.14159265359
using namespace std;
int main() {
double r;
cin >> r;
cout << fixed;
cout.precision(6);
//1. 유클리드 기하학에서 반지름이 R인 원의 넓이
cout << pow(r,2)*pi <<"\n";
//2. 택시 기하학에서 반지름이 R인 원의 넓이
cout << 2.0 * pow(r,2) <<"\n";
return 0;
}성공한 사진!

'오뚝이 개발자 > 알고리즘' 카테고리의 다른 글
| [백준 알고리즘] 10872 팩토리얼 (0) | 2021.12.03 |
|---|---|
| [백준 알고리즘] 1002 터렛 (0) | 2021.12.02 |
| [백준 알고리즘] 4153 직각삼각형 (0) | 2021.12.02 |
| [백준 알고리즘] 3009 네 번째 점 (0) | 2021.12.01 |
| [백준 알고리즘] 1085 직사각형에서 탈출 (0) | 2021.12.01 |




